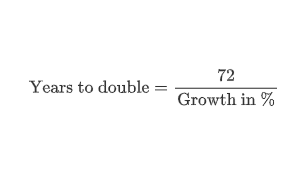Rule of 72
So what is this rule? Should I know about it?
It's a mathematical trick to quickly and easily calculate the doubling time of an investment. See if you can figure out the trick from the table below.
| Compounding % | Years to double |
|---|---|
| 5% | 14.4 |
| 10% | 7.2 |
| 12% | 6 |
| 20% | 3.6 |
Congrats to those who figured it out! The correct rule is:
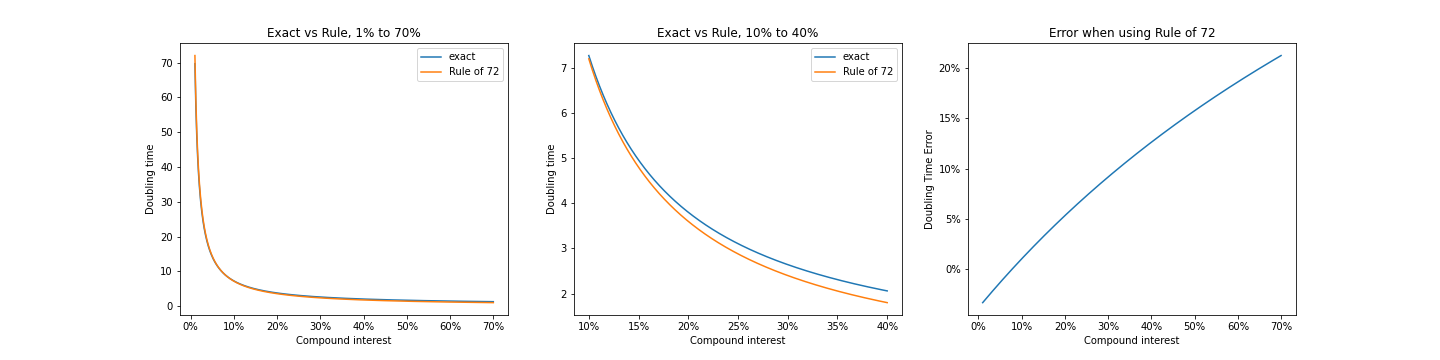
But is it of any use? There are many ways to answer this question, but a quick and revealing one is a python script. Here I check for the error in doubling time. Consider the graphic below:
You can of course not only figure out the doubling time, but also the growth percentage with the Rule of 72. If revenue is doubling every 10 years, that comes to a growth of
But where does it come from?
Let us dive into the subject ourselves and see if we can come up with the answer.
First it will be helpful to figure out the exact answer to the doubling time question. This is very easy
In words: "Twice my capital is my capital, times my growth rate, repeated by the number of years." We want to figure out the number of years, that will then be,
where we used the logarithm. Let's use symbols to make this more compact
To approximate a function, an invaluable tool in mathematics is the Taylor expansion. It looks scary but is actually a factory process once learned. Let's do a Taylor expansion! The way it goes is we pick a point around which we would like to approximate the function. In the case of our function we pick the following point p.
Why did we pick this point? This point represents a percentage (100%), which means our investment does not grow at all, and around that we want to know our answer. It also makes the math much easier because a lot of stuff disappears.
I'll let you take a reverse engineering point of view again. You see if you can figure out the pattern. The Taylor expansion for our function around the point 0 is
We can ignore terms that are quadratic or higher, and then we are left with
Our equation from before now transforms:
Do you recognize that? In the numerator, we get something very similar to 72, and in the denominator, we actually have the growth in %. For instance, with 20% growth we get a doubling time of
years. Why do we not have 72 in the numerator? Well, people decided that 72 would be easier, so in addition to the simplifications above we just replace 69.3 with 72. See the wikipedia article here: Rule of 72 - Wikipedia
Practice this rule, it really becomes 2nd nature if you do it often!
Chris